Power Analysis for the Generic Binomial Test
generic.binom.test.RdCalculates power for the generic binomial test with (optional) Type 1 and Type 2 error plots.
Usage
power.binom.test(size, prob, null.prob = 0.5, alpha = 0.05,
alternative = c("two.sided", "one.sided", "two.one.sided"),
plot = TRUE, verbose = TRUE, pretty = FALSE)Arguments
- size
number of trials (zero or more).
- prob
probability of success on each trial under alternative.
- null.prob
probability of success on each trial under null.
- alpha
type 1 error rate, defined as the probability of incorrectly rejecting a true null hypothesis, denoted as \(\alpha\).
- alternative
direction or type of the hypothesis test: "two.sided", "one.sided", or "two.one.sided". For non-inferiority or superiority tests, add or subtract the margin from the null hypothesis value and use alternative = "one.sided".
- plot
logical;
FALSEswitches off Type 1 and Type 2 error plot.TRUEby default.- verbose
logical; whether the output should be printed on the console.
TRUEby default.- pretty
logical; whether the output should show Unicode characters (if encoding allows for it).
FALSEby default.
Value
- size
number of trials (zero or more).
- prob
probability of success on each trial under alternative.
- null.prob
probability of success on each trial under null.
- binom.alpha
critical value(s).
- power
statistical power \((1-\beta)\).
Examples
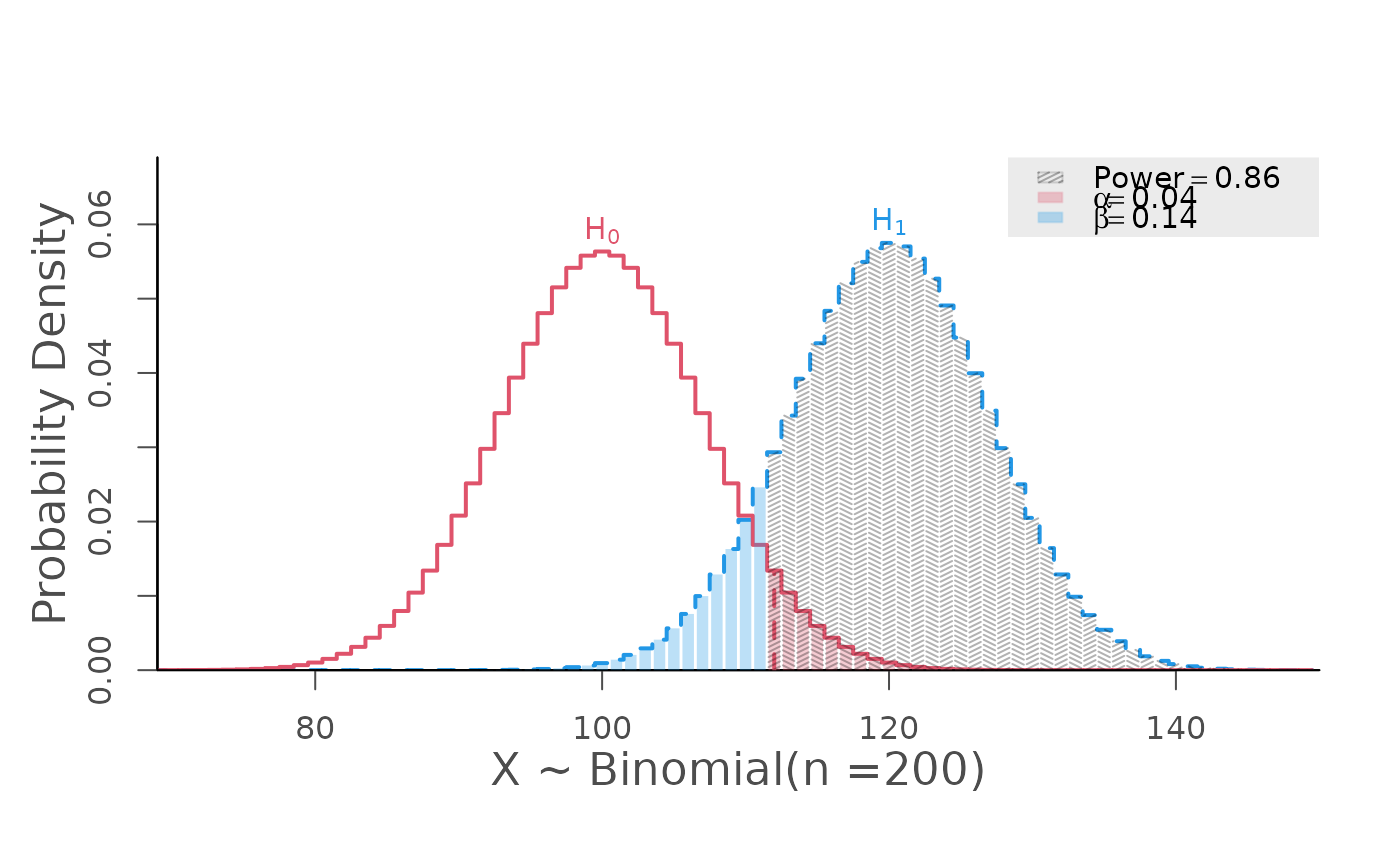
# one-sided
power.binom.test(size = 200, prob = 0.6, null.prob = 0.5,
alpha = 0.05, alternative = "one.sided")
 #> +--------------------------------------------------+
#> | POWER CALCULATION |
#> +--------------------------------------------------+
#>
#> Generic Binomial Test
#>
#> ---------------------------------------------------
#> Hypotheses
#> ---------------------------------------------------
#> H0 (Null Claim) : prob <= null.prob
#> H1 (Alt. Claim) : prob > null.prob
#>
#> ---------------------------------------------------
#> Results
#> ---------------------------------------------------
#> Type 1 Error (alpha) = 0.038
#> Type 2 Error (beta) = 0.140
#> Statistical Power = 0.86 <<
#>
# two-sided
power.binom.test(size = 200, prob = 0.4, null.prob = 0.5,
alpha = 0.05, alternative = "two.sided")
#> +--------------------------------------------------+
#> | POWER CALCULATION |
#> +--------------------------------------------------+
#>
#> Generic Binomial Test
#>
#> ---------------------------------------------------
#> Hypotheses
#> ---------------------------------------------------
#> H0 (Null Claim) : prob <= null.prob
#> H1 (Alt. Claim) : prob > null.prob
#>
#> ---------------------------------------------------
#> Results
#> ---------------------------------------------------
#> Type 1 Error (alpha) = 0.038
#> Type 2 Error (beta) = 0.140
#> Statistical Power = 0.86 <<
#>
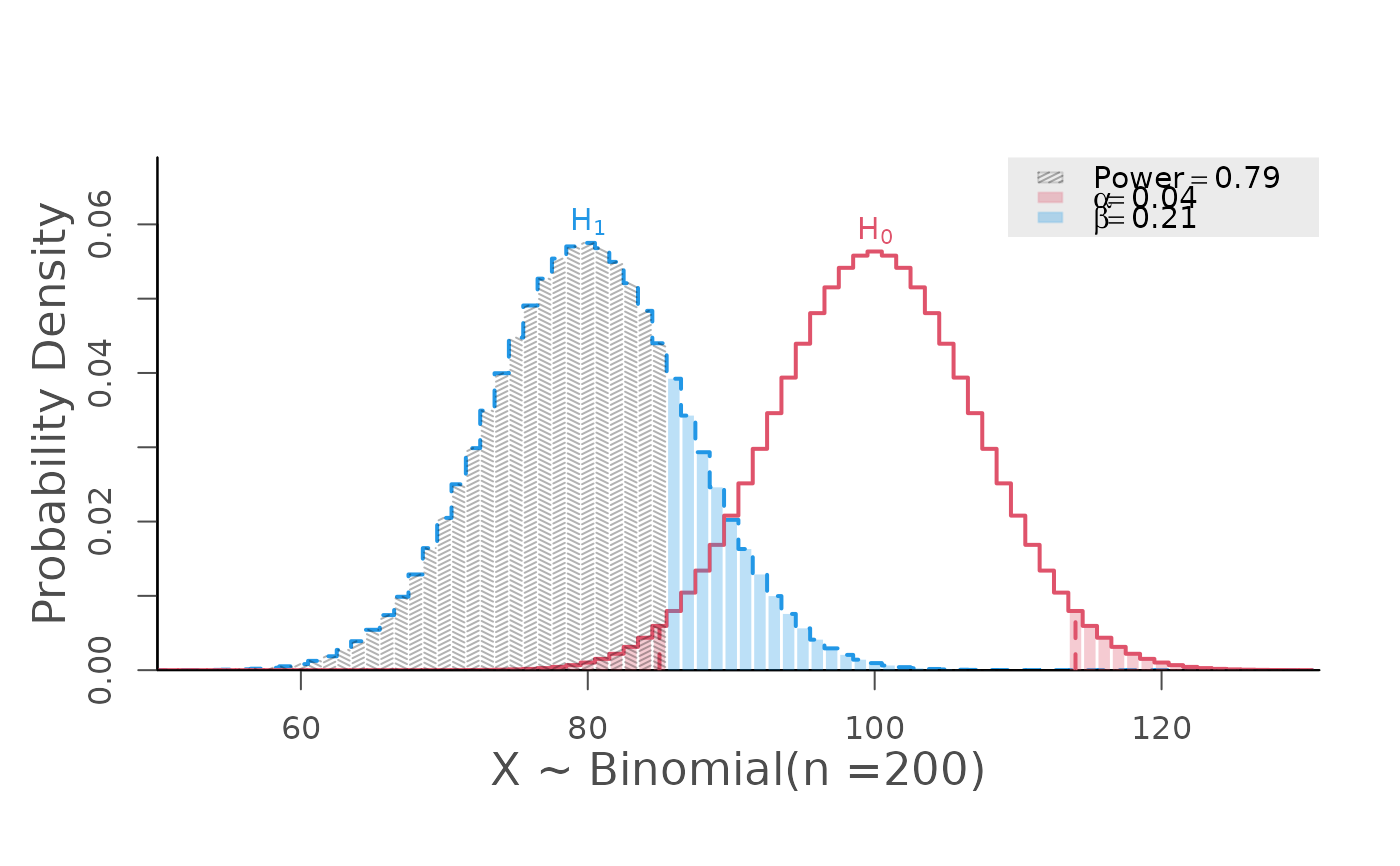
# two-sided
power.binom.test(size = 200, prob = 0.4, null.prob = 0.5,
alpha = 0.05, alternative = "two.sided")
 #> +--------------------------------------------------+
#> | POWER CALCULATION |
#> +--------------------------------------------------+
#>
#> Generic Binomial Test
#>
#> ---------------------------------------------------
#> Hypotheses
#> ---------------------------------------------------
#> H0 (Null Claim) : prob = null.prob
#> H1 (Alt. Claim) : prob != null.prob
#>
#> ---------------------------------------------------
#> Results
#> ---------------------------------------------------
#> Type 1 Error (alpha) = 0.040
#> Type 2 Error (beta) = 0.213
#> Statistical Power = 0.787 <<
#>
# equivalence
power.binom.test(size = 200, prob = 0.5, null.prob = c(0.4, 0.6),
alpha = 0.05, alternative = "two.one.sided")
#> +--------------------------------------------------+
#> | POWER CALCULATION |
#> +--------------------------------------------------+
#>
#> Generic Binomial Test
#>
#> ---------------------------------------------------
#> Hypotheses
#> ---------------------------------------------------
#> H0 (Null Claim) : prob = null.prob
#> H1 (Alt. Claim) : prob != null.prob
#>
#> ---------------------------------------------------
#> Results
#> ---------------------------------------------------
#> Type 1 Error (alpha) = 0.040
#> Type 2 Error (beta) = 0.213
#> Statistical Power = 0.787 <<
#>
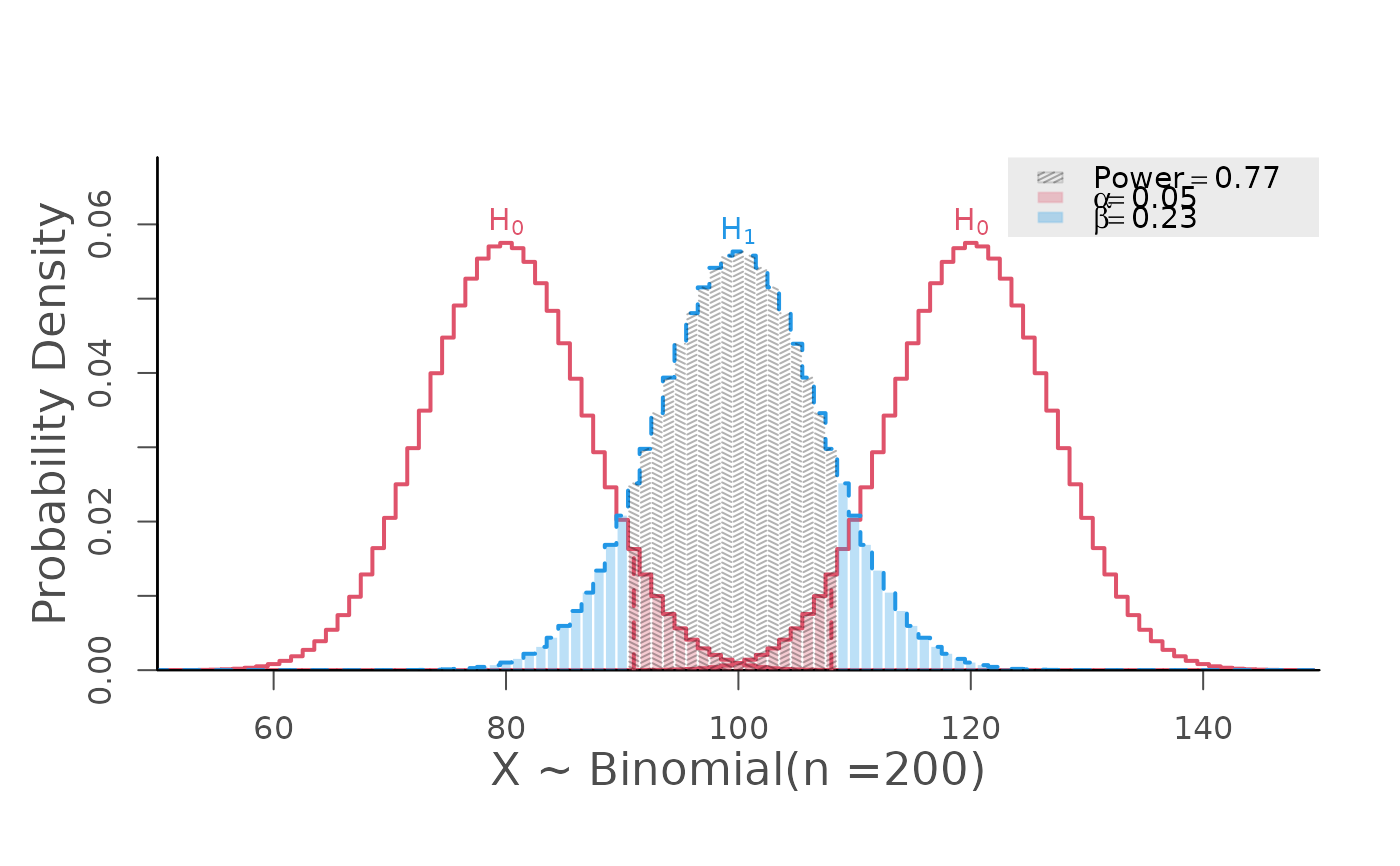
# equivalence
power.binom.test(size = 200, prob = 0.5, null.prob = c(0.4, 0.6),
alpha = 0.05, alternative = "two.one.sided")
 #> +--------------------------------------------------+
#> | POWER CALCULATION |
#> +--------------------------------------------------+
#>
#> Generic Binomial Test
#>
#> ---------------------------------------------------
#> Hypotheses
#> ---------------------------------------------------
#> H0 (Null Claim) : prob <= min(null.prob) or
#> prob >= max(null.prob)
#> H1 (Alt. Claim) : prob > min(null.prob) and
#> prob < max(null.prob)
#>
#> ---------------------------------------------------
#> Results
#> ---------------------------------------------------
#> Type 1 Error (alpha) = 0.049
#> Type 2 Error (beta) = 0.229
#> Statistical Power = 0.771 <<
#>
#> +--------------------------------------------------+
#> | POWER CALCULATION |
#> +--------------------------------------------------+
#>
#> Generic Binomial Test
#>
#> ---------------------------------------------------
#> Hypotheses
#> ---------------------------------------------------
#> H0 (Null Claim) : prob <= min(null.prob) or
#> prob >= max(null.prob)
#> H1 (Alt. Claim) : prob > min(null.prob) and
#> prob < max(null.prob)
#>
#> ---------------------------------------------------
#> Results
#> ---------------------------------------------------
#> Type 1 Error (alpha) = 0.049
#> Type 2 Error (beta) = 0.229
#> Statistical Power = 0.771 <<
#>